HMF 1 - Lösung
Inhaltsverzeichnis
\(\\\)
Aufgabe 1 – Schnittpunkt und Orthogonalität
Wie man sieht, haben beide Geraden
\( \quad g: \vec{x}= \begin{smallmatrix} \left( \begin{array}{r} 3 \\ -3 \\ 3 \end{array} \right) \end{smallmatrix} +r \cdot \begin{smallmatrix} \left( \begin{array}{r} 3 \\ 0 \\ -1 \end{array} \right) \end{smallmatrix} \qquad \text{und} \qquad h: \vec{x}= \begin{smallmatrix} \left( \begin{array}{r} 3 \\ -3 \\ 3 \end{array} \right) \end{smallmatrix} +s \cdot \begin{smallmatrix} \left( \begin{array}{r} 1 \\ 0 \\ 3 \end{array} \right) \end{smallmatrix} %\\[5pt] \)
den gleichen Stützvektor und laufen durch den gemeinsamen Punkt \((3|-3|3)\).
Sind die Geraden orthogonal zueinander, so muss das Skalarprodukt der Richtungsvektoren Null ergeben.
\( \quad \begin{smallmatrix} \left( \begin{array}{r} 3 \\ 0 \\ -1 \end{array} \right) \end{smallmatrix} \circ \begin{smallmatrix} \left( \begin{array}{r} 1 \\ 0 \\ 3 \end{array} \right) \end{smallmatrix} =3 \cdot 1 + 0 \cdot 0 + (-1) \cdot 3 = 0 \\[24pt] \)
Aufgabe 2 – Ebene in Koordinatenform
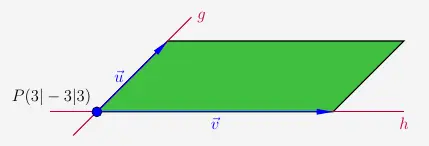
Zunächst stellen wir die Gleichung der Ebene in Parameterform dar mit den Schnittpunkt der Geraden \(g\) und \(h\) als Stützvektor und den Richtungsvektoren der beiden Geraden.
\( \quad Parameterform: \quad \vec{x} = \begin{smallmatrix} \left( \begin{array}{r} 3 \\ -3 \\ 3 \end{array} \right) \end{smallmatrix} +r \cdot \begin{smallmatrix} \left( \begin{array}{r} 3 \\ 0 \\ -1 \end{array} \right) \end{smallmatrix} +s \cdot \begin{smallmatrix} \left( \begin{array}{r} 1 \\ 0 \\ 3 \end{array} \right) \end{smallmatrix} \)
\(\\\) Diese formen wir um in die Normalenform von der Art
\( \quad (\vec{x} - \vec{p}) \circ \vec{n} = 0 , \)
\(\\\)
wobei als \(\vec{p}\) der Stützvektor genommen wird. Der Normalenvektor wird gebildet aus dem Kreuzprodukt der beiden Richtungsvektoren \(\vec{u}\) und \(\vec{v}\)
\( \quad \begin{array}{ r c l} \vec{n} & = & \vec{u} \times \vec{v} \\ \\ \vec{n} & = & \begin{smallmatrix} \left( \begin{array}{r} 3 \\ 0 \\ -1 \end{array} \right) \end{smallmatrix} \times \begin{smallmatrix} \left( \begin{array}{r} 1 \\ 0 \\ 3 \end{array} \right) \end{smallmatrix} \\ \end{array} \)
\(\\\) und wird berechnet auf folgende Weise:
Die beiden Richtungsvektoren werden paarweise 2-mal untereinander geschrieben. Die erste und die letzte Zeile werden gestrichen. Dann wird über Kreuz multipliziert und jeweils die blaue Diagonale (Hauptdiagonale) minus die rote Diagonale (Nebendiagonale) gerechnet.

Der Normalenvektor lautet \( \begin{smallmatrix} \left( \begin{array}{r} 0 \\ -10 \\ 0 \end{array} \right) \end{smallmatrix} \\ \)
\(\\\)
Wir vereinfachen den Normalenvektor indem wir ihn durch -10 teilen und erhalten \( \begin{smallmatrix} \left( \begin{array}{r} 0 \\ 1 \\ 0 \end{array} \right) \end{smallmatrix} \\ \)
Daraus ergibt sich die
\( \quad \begin{array}{ c} Normalenform: \quad \left[ \vec{x} - \begin{smallmatrix} \left( \begin{array}{r} 3 \\ -3 \\ 3 \end{array} \right) \end{smallmatrix} \right] \circ \begin{smallmatrix} \left( \begin{array}{r} 0 \\ 1 \\ 0 \end{array} \right) \end{smallmatrix} = 0 \end{array} \\[5pt] \)
Um weiter in die Koordinatenform zu kommen, lösen wir das Skalarprodukt auf.
\( \quad \begin{align} \left[ \begin{smallmatrix} \left( \begin{array}{r} x_1 \\ x_2 \\ x_3 \end{array} \right) \end{smallmatrix} -\begin{smallmatrix} \left( \begin{array}{r} 3 \\ -3 \\ 3 \end{array} \right) \end{smallmatrix} \right] \circ \begin{smallmatrix} \left( \begin{array}{r} 0 \\ 1 \\ 0 \end{array} \right) \end{smallmatrix} & = 0 \\[8pt] \begin{smallmatrix} \left( \begin{array}{r} x_1 \\ x_2 \\ x_3 \end{array} \right) \end{smallmatrix} \circ \begin{smallmatrix} \left( \begin{array}{r} 0 \\ 1 \\ 0 \end{array} \right) \end{smallmatrix} -\begin{smallmatrix} \left( \begin{array}{r} 3 \\ -3 \\ 3 \end{array} \right) \end{smallmatrix} \circ \begin{smallmatrix} \left( \begin{array}{r} 0 \\ 1 \\ 0 \end{array} \right) \end{smallmatrix} & = 0 \\[8pt] x_1 \cdot 0 + x_2 \cdot 1 + x_3 \cdot 0 - \big(3 \cdot 0 + (-3) \cdot 1 + 3 \cdot 0 \big) & = 0 \\[5pt] x_2 - (-3) & = 0 \\[5pt] x_2 +3 & = 0 \qquad |-3\\[5pt] x_2 & = -3 \qquad \Rightarrow \quad \text{Koordinatenform} \end{align} \)
\(\\\)